Last updated: 2023-06-05
Checks: 6 1
Knit directory:
Diversidade-gen-tica-e-identifica-o-de-regi-es-gen-micas-associadas-ao-tamanho-dos-gr-nulos-de-amid/
This reproducible R Markdown analysis was created with workflowr (version 1.7.0). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
The R Markdown file has unstaged changes. To know which version of
the R Markdown file created these results, you’ll want to first commit
it to the Git repo. If you’re still working on the analysis, you can
ignore this warning. When you’re finished, you can run
wflow_publish to commit the R Markdown file and build the
HTML.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20230313) was run prior to running
the code in the R Markdown file. Setting a seed ensures that any results
that rely on randomness, e.g. subsampling or permutations, are
reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.
The results in this page were generated with repository version c7737db. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.
Note that you need to be careful to ensure that all relevant files for
the analysis have been committed to Git prior to generating the results
(you can use wflow_publish or
wflow_git_commit). workflowr only checks the R Markdown
file, but you know if there are other scripts or data files that it
depends on. Below is the status of the Git repository when the results
were generated:
Ignored files:
Ignored: .RData
Ignored: .Rhistory
Ignored: .Rproj.user/
Untracked files:
Untracked: analysis/cap2.Rmd
Untracked: cluster.png
Untracked: cor_heatmap.png
Untracked: correlation.png
Untracked: data/dados_RVA_final.xlsx
Untracked: output/BLUPS.RData
Untracked: output/BLUPS.Rdata
Untracked: output/Cluster_a_priori.txt
Untracked: output/Clusters.txt
Untracked: output/Correlacao.txt
Untracked: output/Prob_a_posteriori.txt
Untracked: output/boxplot_violine.tiff
Untracked: output/cluster.png
Untracked: output/cor_heatmap.png
Untracked: output/correlation.png
Untracked: output/density_BLUPS.tiff
Untracked: output/mean_germ_cluster.txt
Untracked: output/parametros.Rdata
Untracked: output/parametros.csv
Untracked: output/varcomp.tiff
Untracked: output/vcomp.Rdata
Untracked: output/vcomp.csv
Unstaged changes:
Modified: .Rprofile
Modified: .gitattributes
Modified: .gitignore
Modified: Diversidade-gen-tica-e-identifica-o-de-regi-es-gen-micas-associadas-ao-tamanho-dos-gr-nulos-de-amid.Rproj
Modified: README.html
Modified: README.md
Modified: _workflowr.yml
Modified: analysis/_site.yml
Modified: analysis/about.Rmd
Modified: analysis/index.Rmd
Modified: analysis/license.Rmd
Modified: code/README.md
Modified: data/README.md
Modified: data/dados_gwas.csv
Modified: output/README.md
Deleted: output/boxplot-H2.tiff
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the repository in which changes were
made to the R Markdown (analysis/index.Rmd) and HTML
(docs/index.html) files. If you’ve configured a remote Git
repository (see ?wflow_git_remote), click on the hyperlinks
in the table below to view the files as they were in that past version.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | c7737db | WevertonGomesCosta | 2023-06-01 | Update index |
| Rmd | e414958 | WevertonGomesCosta | 2023-06-01 | Update Readme |
| Rmd | ce058e7 | WevertonGomesCosta | 2023-06-01 | Update data, about and license |
| Rmd | cf18bdb | WevertonGomesCosta | 2023-05-29 | Analisys Blups |
| Rmd | 264f03e | WevertonGomesCosta | 2023-03-13 | Start workflowr project. |
Variabilidade genética de acessos de mandioca para tamanho e formato dos grãos e suas implicações nas propriedades de pasta
Este projeto tem como objetivo realizar uma análise da diversidade genética do tamanho dos grânulos de amido na cultura da mandioca. Serão utilizados dados coletados em diferentes anos, visando identificar a variação existente nos genótipos da mandioca.
Pacotes
Nesta análise, utilizaremos os seguintes pacotes do R:
# Pacotes para manipulação e visualização de dados
library(tidyverse) # Conjunto de pacotes para manipulação e visualização de dados
library(DataExplorer) # Ferramentas para análise exploratória de dados
library(kableExtra) # Melhorias para a criação de tabelas
# Pacotes para análise estatística
library(metan) # Meta-análise
library(factoextra) # Ferramentas para análise de fatores e agrupamentos
library(adegenet)
# Pacotes para visualização de dados
library(RColorBrewer) # Esquemas de cores personalizados
library(corrplot) # Visualização de matrizes de correlação
library(gplots) # Ferramentas para visualização de dados
library(compiler) # Compilação de funções para melhorar a velocidade de execução
library(scatterplot3d) # Gráficos de dispersão em 3D
library(ComplexHeatmap) # Visualização de dados complexos em heatmap
library(circlize) # Visualização circular de dados
library(dendextend) # Extensões para manipulação de dendrogramas
# Pacotes para paralelização e iteração
library(doParallel)
library(foreach)
# Pacotes adicionais para gráficos e estatísticas
library(ggthemes) # Temas adicionais para gráficos ggplot2
library(GGally) # Ferramentas para visualização de gráficos de matriz com o ggplot2
library(PMCMRplus) # Comparação em pares
library(ggstatsplot) # Gráficos estatísticos interativos
library(rstatix)Análise Descritiva
Nesta etapa, serão realizadas as seguintes tarefas:
Leitura e pré-processamento dos dados
Os dados são lidos a partir do arquivo “dados_RVA.xlsx” e passam por um processo de pré-processamento. Isso inclui a limpeza dos nomes das colunas, a seleção das variáveis relevantes, a transformação dos tipos de dados, a remoção de valores ausentes e o cálculo da média para as variáveis numéricas. Também são realizadas outras transformações nos dados, como a conversão de fatores e a filtragem de registros com valores inválidos.
nomes_corretos <-
readxl::read_xlsx("data/Label Taxa nome dos clones GBS DART CHIP.xlsx") %>%
mutate_if(is.logical, as.character) %>%
pivot_longer(cols = c(2, 7:13),
names_to = "synonyms",
values_to = "BAD_NAME") %>%
select(`GOOD NAME`, BAD_NAME) %>%
rename(amostras = BAD_NAME) %>%
count(`GOOD NAME`, amostras) %>%
na.omit() %>%
select(1,2)
dados <- readxl::read_xlsx("data/dados_RVA_final.xlsx") %>%
janitor::clean_names() %>%
select(amostras, ano, ensaio, repeticao:pasting_temp) %>%
mutate_if(is.character, as.factor) %>%
left_join(nomes_corretos) %>%
mutate(repeticao = as.factor(ifelse(repeticao %% 2 == 0, 1, 2)),
ano = as.factor(ano),
amostras = ifelse(is.na(`GOOD NAME`), amostras, `GOOD NAME`)) %>%
group_by(amostras, ano, ensaio, repeticao) %>%
summarise_if(is.numeric, mean, na.rm = TRUE) %>%
ungroup() %>%
distinct()Contagem de genótipos
Nesta etapa, é realizada a contagem de genótipos que foram avaliados para cada ano.
# Contagem de genótipos
dados2 <- dados %>%
count(amostras) %>%
count(n) %>%
arrange(n)
# Tabela com contagem de genótipos
dados2 %>%
kbl(
escape = FALSE,
align = 'c',
col.names = c("Nº de Genótipos", "Contagem")
) %>%
kable_classic(
"hover",
full_width = FALSE,
position = "center",
fixed_thead = TRUE
)| Nº de Genótipos | Contagem |
|---|---|
| 1 | 169 |
| 2 | 872 |
| 3 | 29 |
| 4 | 102 |
| 5 | 1 |
| 6 | 7 |
| 8 | 1 |
A maioria dos genótipos foram repetidos em mais de um ano, o que é desejável para a análise.
Contagem de genótipos por ano
Nesta etapa, é realizada a contagem do número de genótipos para cada ano. O objetivo é identificar a quantidade de genótipos presentes em cada ano de coleta dos dados.
# Contagem de genótipos por ano
dados2 <- dados %>%
count(ano, amostras)
# Tabela com contagem de genótipos por ano
dados2 %>%
group_by(ano) %>%
summarise(`Nº de genótipos` = length(amostras)) %>%
kbl(
escape = FALSE,
align = 'c',
col.names = c("Ano", "Nº de genótipos")
) %>%
kable_classic(
"hover",
full_width = FALSE,
position = "center",
fixed_thead = TRUE
)| Ano | Nº de genótipos |
|---|---|
| 2011 | 476 |
| 2012 | 383 |
| 2013 | 171 |
| 2017 | 7 |
| 2018 | 3 |
| 2019 | 101 |
| 2020 | 102 |
| 2021 | 73 |
| 2022 | 9 |
Observamos que os anos de 2017, 2018 e 2020 são os anos com a menor quantidade de genótipos. No entanto, continuaremos a análise descritiva para verificar se isso será algo problemático.
dados2<- dados %>%
count(ano, amostras)
genmat = model.matrix( ~ -1 + amostras, data = dados2)
envmat = model.matrix( ~ -1 + ano, data = dados2)
genenvmat = t(envmat) %*% genmat
genenvmat_ch = ifelse(genenvmat == 1, "Present", "Abscent")
genenvmat %*% t(genenvmat) %>%
kbl(escape = F,
align = 'c') %>%
kable_classic(
"hover",
full_width = F,
position = "center",
fixed_thead = T
)| ano2011 | ano2012 | ano2013 | ano2017 | ano2018 | ano2019 | ano2020 | ano2021 | ano2022 | |
|---|---|---|---|---|---|---|---|---|---|
| ano2011 | 476 | 0 | 0 | 0 | 1 | 26 | 11 | 14 | 0 |
| ano2012 | 0 | 383 | 1 | 0 | 0 | 21 | 18 | 12 | 0 |
| ano2013 | 0 | 1 | 171 | 0 | 0 | 7 | 16 | 10 | 0 |
| ano2017 | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 |
| ano2018 | 1 | 0 | 0 | 0 | 3 | 0 | 1 | 1 | 0 |
| ano2019 | 26 | 21 | 7 | 0 | 0 | 101 | 4 | 1 | 0 |
| ano2020 | 11 | 18 | 16 | 0 | 1 | 4 | 102 | 7 | 0 |
| ano2021 | 14 | 12 | 10 | 0 | 1 | 1 | 7 | 73 | 1 |
| ano2022 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 9 |
Não houve nenhum clone reptido em todos os anos.
Distribuição de ensaios e repetição por ano
Em seguida, verificamos a distribuição das características por ano
utilizando a função plot_bar com o argumento
by = "ano". Isso nos permite gerar gráficos de barras que
mostram a distribuição dos valores de cada variável em cada ano.
plot_bar(dados, by = "ano", ggtheme = theme_gdocs())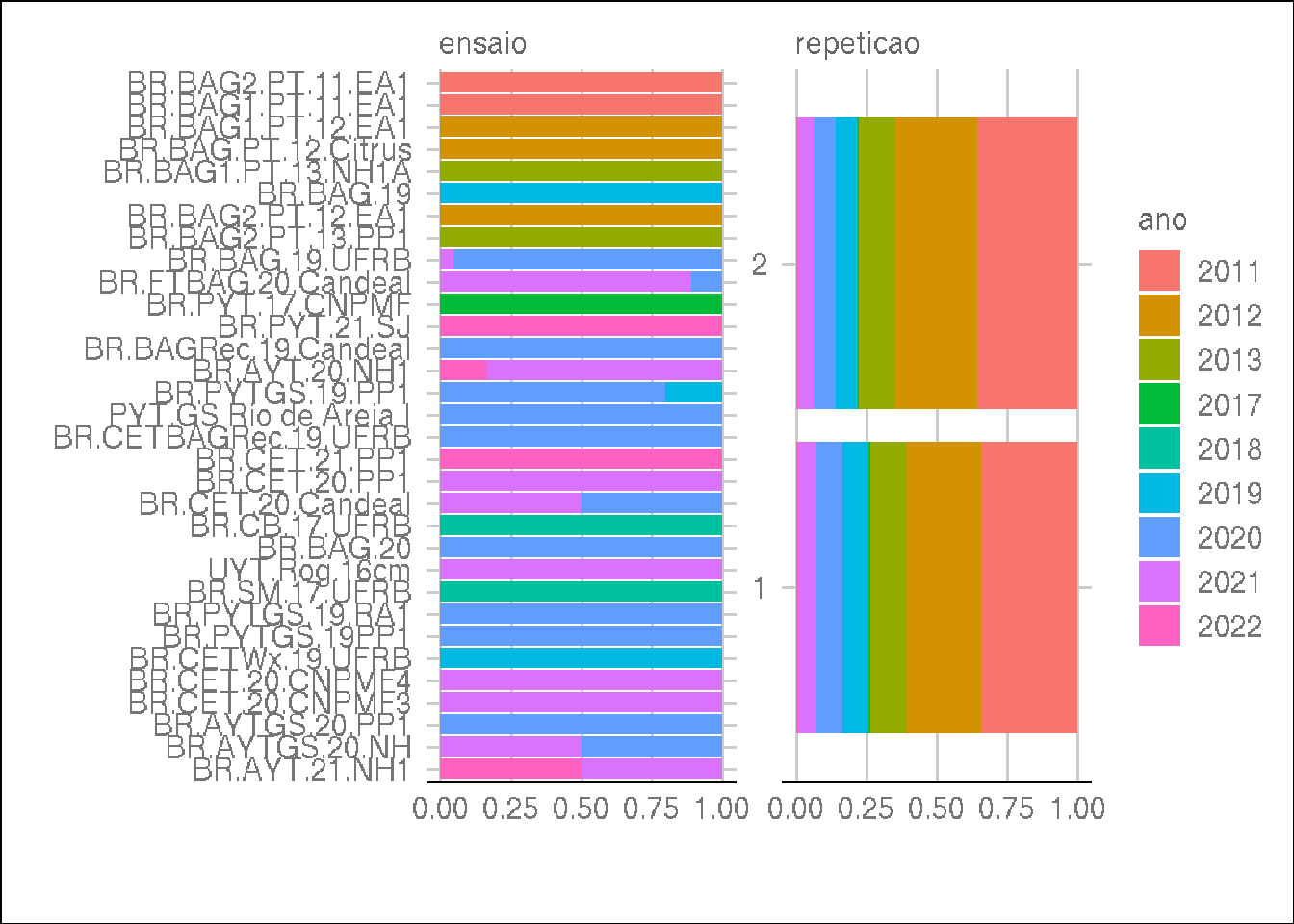
Ao observar os resultados, identificamos que alguns ensaios possuem anos diferentes na coleta dos dados. Mas como o ano indica o ano de extração do amido e no máximo poderia ter sido obtido no ano posterior, como é o caso de todos os ensaios, vamos manter os dados assim.
Análise das variáveis
Realizamos uma análise das variáveis presentes nos dados, buscando entender a distribuição e características de cada uma delas.
Primeiramente, observamos um resumo dos dados pelas medidas descritivas.
# Resumo dos dados pelas medidas descritivas
summary(dados) %>%
kbl(
escape = FALSE,
align = 'c'
) %>%
kable_classic(
"hover",
full_width = FALSE,
position = "center",
fixed_thead = TRUE
)| amostras | ano | ensaio | repeticao | peak_visc | min_visc_afheat | breakdown | final_visc | setback | pasting_temp | |
|---|---|---|---|---|---|---|---|---|---|---|
| Length:2463 | 2011 :864 | BR.BAG2.PT.11.EA1 :450 | 1:1132 | Min. :2832 | Min. : 208 | Min. :1414 | Min. : 246 | Min. : 38 | Min. :59.27 | |
| Class :character | 2012 :687 | BR.BAG1.PT.11.EA1 :414 | 2:1331 | 1st Qu.:4371 | 1st Qu.:1498 | 1st Qu.:2780 | 1st Qu.:2414 | 1st Qu.: 822 | 1st Qu.:68.70 | |
| Mode :character | 2013 :312 | BR.BAG1.PT.12.EA1 :290 | NA | Median :4729 | Median :1674 | Median :3032 | Median :2743 | Median :1048 | Median :70.20 | |
| NA | 2020 :210 | BR.BAG.PT.12.Citrus:229 | NA | Mean :4696 | Mean :1654 | Mean :3042 | Mean :2662 | Mean :1033 | Mean :70.01 | |
| NA | 2019 :202 | BR.BAG1.PT.13.NH1A :222 | NA | 3rd Qu.:5041 | 3rd Qu.:1844 | 3rd Qu.:3294 | 3rd Qu.:3006 | 3rd Qu.:1255 | 3rd Qu.:71.05 | |
| NA | 2021 :150 | BR.BAG.19 :198 | NA | Max. :7372 | Max. :2603 | Max. :5276 | Max. :3822 | Max. :2472 | Max. :75.25 | |
| NA | (Other): 38 | (Other) :660 | NA | NA’s :26 | NA’s :26 | NA’s :26 | NA’s :26 | NA’s :26 | NA’s :26 |
Para peak_visc a setback, podemos observar uma discrepância dos valores mínimos até o 1º quartil, ou seja, esses dados possivelmente serão considerados outliers.
Prosseguindo com a análise, avaliaremos a distribuição por ano utilizando a função plot_boxplot, agora agrupando os dados por ano.
# Distribuição por ano usando boxplots
plot_boxplot(
dados,
by = "ano",
nrow = 4,
ggtheme = theme_gdocs(),
geom_boxplot_args = list(outlier.colour = "red", outlier.shape = 1)
)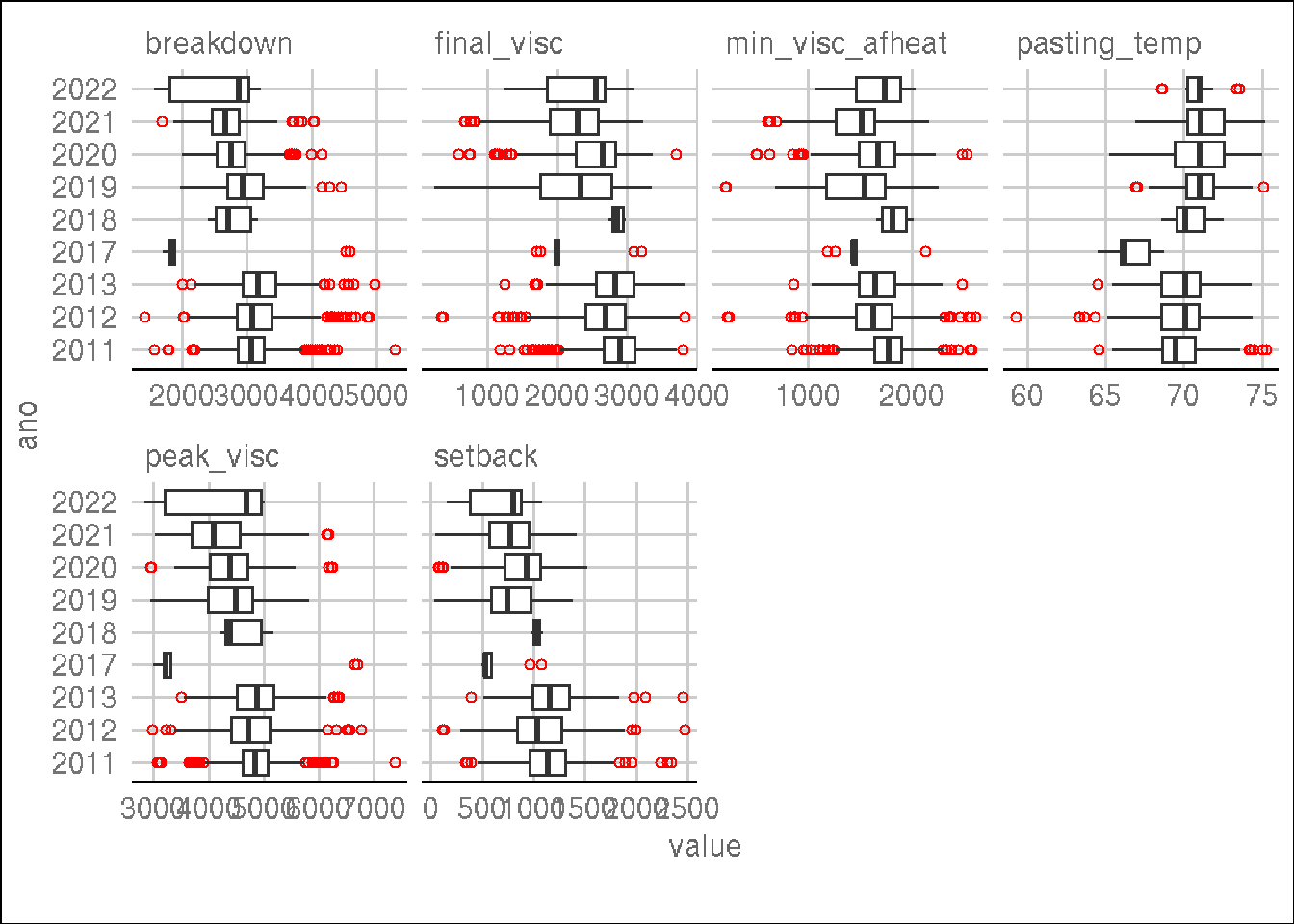
O ano de 2017 apresenta uma baixa variação para a maioria das características, mas segue dentro do esperado quando comparado com os demais anos. Assim, iremos prosseguir inicialmente com todos os dados.
Análise das amostras
Nesta etapa, realizamos uma análise das amostras presentes nos ensaios, com o objetivo de verificar detalhes dos dados e identificar possíveis problemas ou discrepâncias.
Primeiramente, verificamos os detalhes dos dados por ensaio para todas as variáveis. Utilizamos a função ge_details para obter informações como média, desvio padrão, mínimo, máximo e contagem de valores ausentes para cada variável e ensaio.
# Detalhes dos dados por ensaio
ge_details(dados, ano, amostras, resp = everything()) %>%
t() %>%
kbl(escape = FALSE, align = 'c') %>%
kable_classic(
"hover",
full_width = FALSE,
position = "center",
fixed_thead = TRUE
)| Parameters | Mean | SE | SD | CV | Min | Max | MinENV | MaxENV | MinGEN | MaxGEN |
| peak_visc | 4695.74 | 11.5 | 567.63 | 12.09 | 2832 (BR-19F2Wx-356-2 in 2022) | 7372 (BGM-0327 in 2011) | 2017 (3699.57) | 2013 (4858.82) | BR-19F2Wx-356-2 (2836.5) | BGM-2025 (6676.5) |
| min_visc_afheat | 1654.17 | 5.89 | 290.6 | 17.57 | 208 (BGM-0895 in 2019) | 2603 (BGM-1158 in 2012) | 2021 (1448.89) | 2018 (1827.33) | BGM-0942 (506) | BGM-1158 (2581.25) |
| breakdown | 3041.57 | 8.9 | 439.21 | 14.44 | 1414 (BGM-1177 in 2012) | 5276 (BGM-0327 in 2011) | 2017 (2194.43) | 2013 (3200.2) | BGM-1177 (1418.5) | BGM-1403 (4865.5) |
| final_visc | 2662.11 | 10.5 | 518 | 19.46 | 246 (BGM-0895 in 2019) | 3822 (BGM-0958 in 2012) | 2017 (2113.86) | 2018 (2859) | BGM-0942 (581.5) | BGM-0958 (3822) |
| setback | 1032.87 | 6.58 | 324.79 | 31.45 | 38 (BGM-0895 in 2019) | 2472 (BGM-1123 in 2012) | 2017 (608.71) | 2013 (1172.46) | BGM-0971 (46.5) | BGM-1123 (2233) |
| pasting_temp | 70.01 | 0.04 | 1.76 | 2.52 | 59.27 (BGM-1410 in 2012) | 75.25 (BGM-0495 in 2011) | 2017 (66.71) | 2021 (71.2) | BGM-1407 (63.31) | BGM-0808 (75.2) |
Observamos que a variável setback apresenta coeficiente de variação (CV) alto, indicando uma maior variabilidade e possíveis valores discrepantes em alguns anos. Além disso o clone BGM-0895 no ano de 2017 apresentou menores valores para várias cracterísticas vamos eliminá-lo e verificar novamente os detalhes dos dados.
dados <- dados %>%
filter(amostras != "BGM-0895") %>%
droplevels()
# Detalhes dos dados por ensaio
ge_details(dados, ano, amostras, resp = everything()) %>%
t() %>%
kbl(escape = FALSE, align = 'c') %>%
kable_classic(
"hover",
full_width = FALSE,
position = "center",
fixed_thead = TRUE
)| Parameters | Mean | SE | SD | CV | Min | Max | MinENV | MaxENV | MinGEN | MaxGEN |
| peak_visc | 4697.26 | 11.47 | 565.87 | 12.05 | 2832 (BR-19F2Wx-356-2 in 2022) | 7372 (BGM-0327 in 2011) | 2017 (3699.57) | 2013 (4858.82) | BR-19F2Wx-356-2 (2836.5) | BGM-2025 (6676.5) |
| min_visc_afheat | 1655.56 | 5.84 | 287.79 | 17.39 | 228 (BGM-0729 in 2012) | 2603 (BGM-1158 in 2012) | 2021 (1448.89) | 2018 (1827.33) | BGM-0942 (506) | BGM-1158 (2581.25) |
| breakdown | 3041.7 | 8.91 | 439.46 | 14.45 | 1414 (BGM-1177 in 2012) | 5276 (BGM-0327 in 2011) | 2017 (2194.43) | 2013 (3200.2) | BGM-1177 (1418.5) | BGM-1403 (4865.5) |
| final_visc | 2664.4 | 10.42 | 513.68 | 19.28 | 338 (BGM-0729 in 2012) | 3822 (BGM-0958 in 2012) | 2017 (2113.86) | 2018 (2859) | BGM-0942 (581.5) | BGM-0958 (3822) |
| setback | 1033.81 | 6.57 | 323.78 | 31.33 | 45 (BGM-0971 in 2021) | 2472 (BGM-1123 in 2012) | 2017 (608.71) | 2013 (1172.46) | BGM-0971 (46.5) | BGM-1123 (2233) |
| pasting_temp | 70.02 | 0.04 | 1.77 | 2.52 | 59.27 (BGM-1410 in 2012) | 75.25 (BGM-0495 in 2011) | 2017 (66.71) | 2021 (71.2) | BGM-1407 (63.31) | BGM-0808 (75.2) |
Também realizamos uma inspeção visual dos dados, removendo as colunas
referentes às amostras e aos anos. Utilizamos a função
inspect para gerar uma visualização dos dados em forma de
tabela, com a opção de exibir gráficos para uma melhor compreensão. Os
resultados são apresentados em uma tabela formatada.
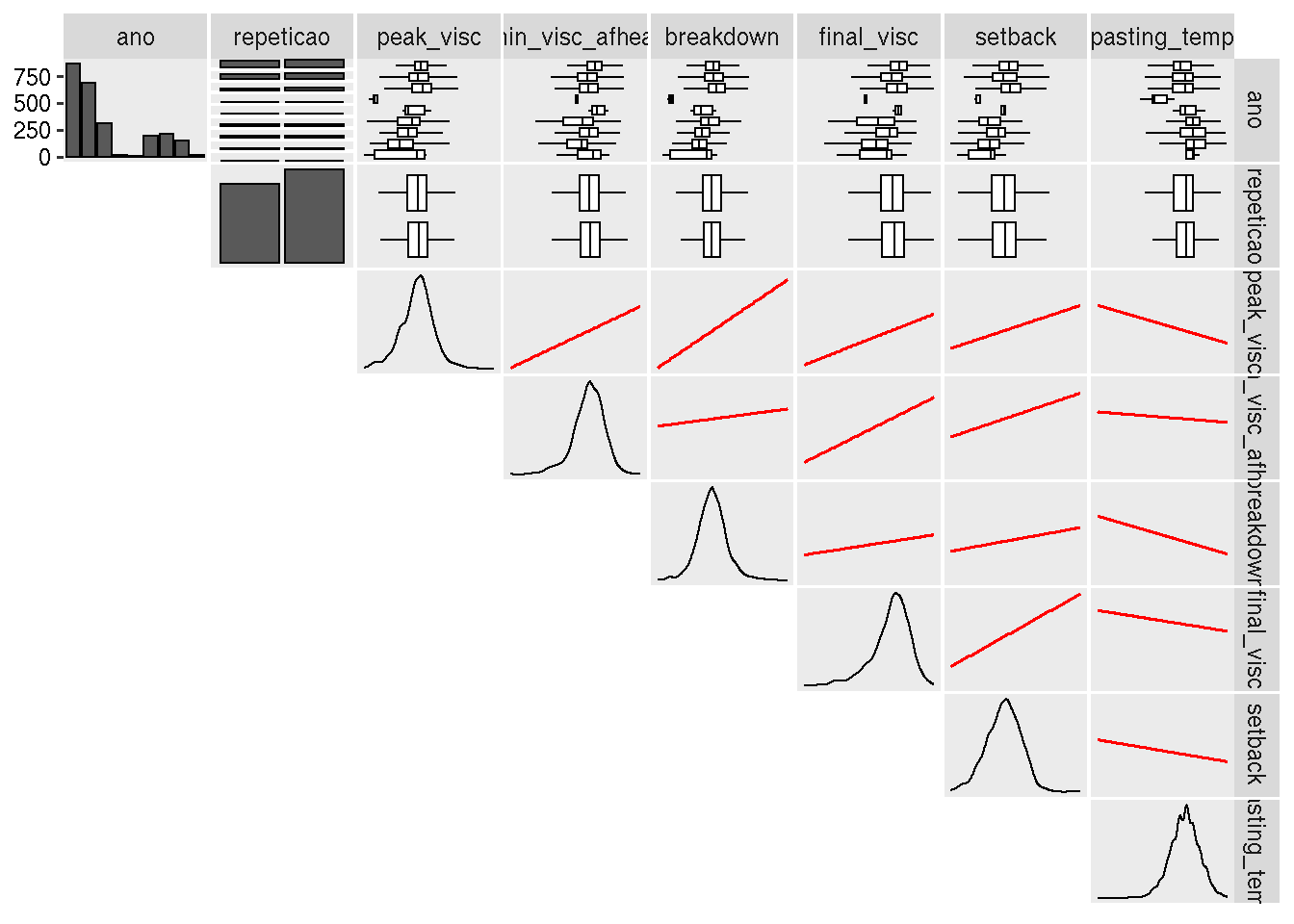
dados %>%
select(-amostras, -ensaio) %>%
inspect(verbose = FALSE, plot = TRUE) %>%
kbl(escape = FALSE, align = 'c') %>%
kable_classic(
"hover",
full_width = FALSE,
position = "center",
fixed_thead = TRUE
)
| Variable | Class | Missing | Levels | Valid_n | Min | Median | Max | Outlier | Text |
|---|---|---|---|---|---|---|---|---|---|
| ano | factor | No | 9 | 2459 | NA | NA | NA | NA | NA |
| repeticao | factor | No | 2 | 2459 | NA | NA | NA | NA | NA |
| peak_visc | numeric | Yes |
|
2433 | 2832.00 | 4729.5 | 7372.00 | 83 | NA |
| min_visc_afheat | numeric | Yes |
|
2433 | 228.00 | 1675.0 | 2603.00 | 83 | NA |
| breakdown | numeric | Yes |
|
2433 | 1414.00 | 3032.5 | 5276.00 | 82 | NA |
| final_visc | numeric | Yes |
|
2433 | 338.00 | 2744.0 | 3822.00 | 89 | NA |
| setback | numeric | Yes |
|
2433 | 45.00 | 1049.0 | 2472.00 | 24 | NA |
| pasting_temp | numeric | Yes |
|
2433 | 59.27 | 70.2 | 75.25 | 15 | NA |
Em seguida, analisamos os histogramas das variáveis quantitativas.
Utilizamos a função plot_histogram para gerar histogramas
que mostram a distribuição dos valores de cada variável
quantitativa.
plot_histogram(dados, ggtheme = theme_gdocs())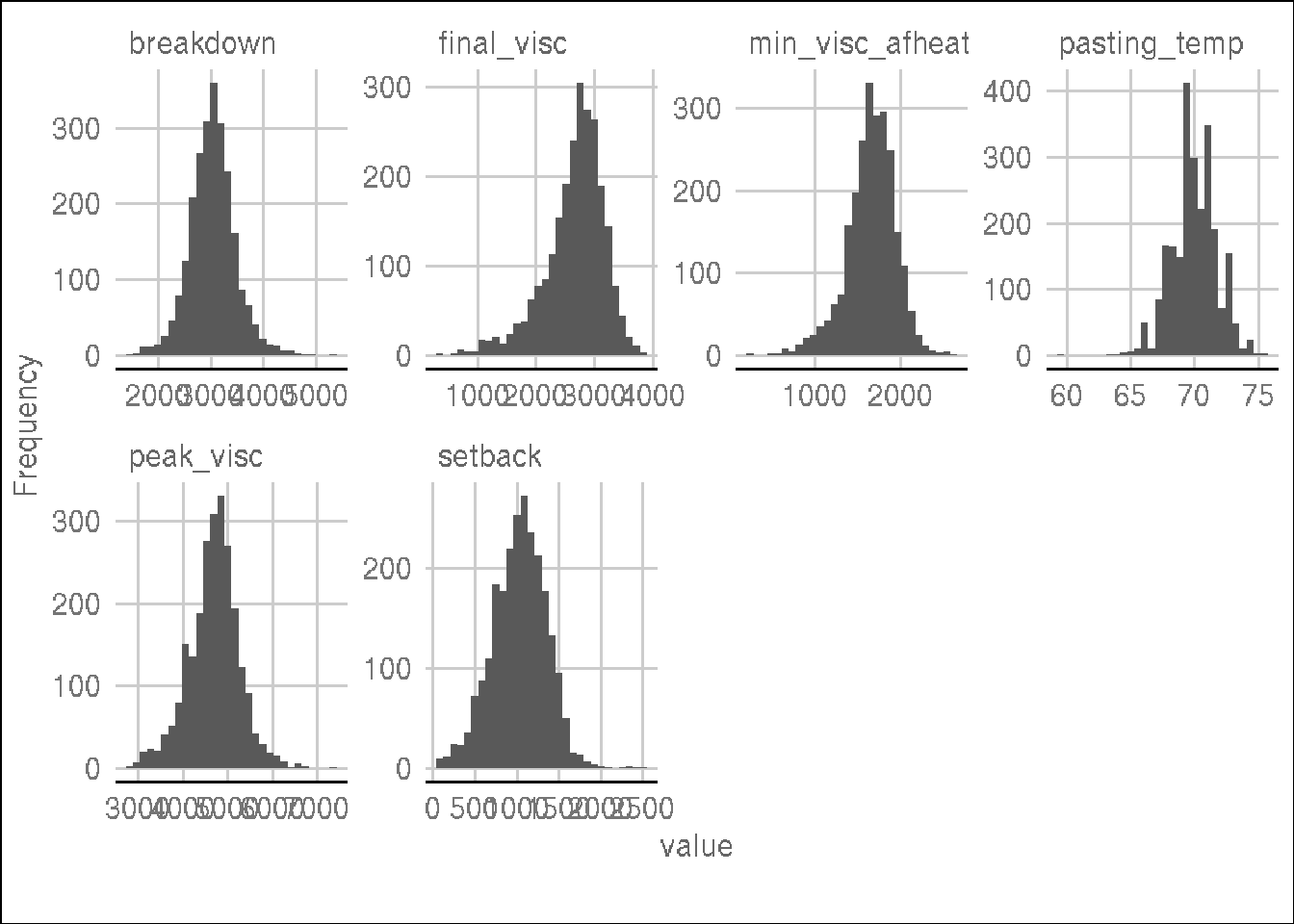
Ao examinar os histogramas, identificamos que as variáveis aparentemente seguem uma distribuição normal. Portanto, podemos prosseguir com a análise de modelos mistos.
Modelos Mistos
Função para obter os parâmetros
A função analise_metan_joint é definida para realizar a análise de metan em um modelo misto específico. Ela extrai os parâmetros de interesse, como a herdabilidade (H2), os valores BLUPs e os valores preditos. Os resultados são retornados como um tibble.
analise_metan_joint <- function(model, trait) {
H2 <- get_model_data(model, "genpar") %>%
filter(Parameters == "Heritability") %>%
pull(trait)
vcomp <- get_model_data(model, what = "vcomp")
parameters <- get_model_data(model)
BLUPS <- get_model_data(model, "ranef")$GEN
Predicted_values <- predict(model) %>%
group_by(GEN) %>%
summarise(across(where(is.numeric), mean)) %>%
pull(trait)
return(
tibble(
trait = trait,
H2 = H2,
germplasmName = BLUPS[[1]],
BLUPS = BLUPS[[2]],
parameters = list(parameters),
vcomp = list(vcomp),
Predicted = Predicted_values
)
)
}Obtenção dos BLUPs
Nesta etapa, realizamos a obtenção dos valores BLUPs (melhores predições lineares não viesadas) para cada característica (trait) utilizando modelos mistos. O processo é realizado em paralelo, utilizando múltiplos núcleos de processamento para otimizar a velocidade de execução.
traits <- colnames(dados)[5:ncol(dados)]
# Registrar os núcleos a serem usados
registerDoParallel(cores = detectCores())
# Loop externo
BLUPS_join <-
foreach(
trait = traits,
.combine = bind_rows,
.multicombine = TRUE,
.verbose = TRUE
) %dopar% {
library(dplyr)
library(metan)
DRG <- list()
data <- dados %>%
select(1:4, all_of(trait)) %>%
na.omit() %>%
droplevels()
model <-
gamem_met(
data,
env = ano,
gen = amostras,
rep = repeticao,
resp = sym(trait)
)
drg <- list(analise_metan_joint(model, trait))
DRG <- append(DRG, drg)
}numValues: 6, numResults: 0, stopped: TRUE
got results for task 1
numValues: 6, numResults: 1, stopped: TRUE
returning status FALSE
got results for task 2
numValues: 6, numResults: 2, stopped: TRUE
returning status FALSE
got results for task 3
numValues: 6, numResults: 3, stopped: TRUE
returning status FALSE
got results for task 4
numValues: 6, numResults: 4, stopped: TRUE
returning status FALSE
got results for task 5
numValues: 6, numResults: 5, stopped: TRUE
returning status FALSE
got results for task 6
numValues: 6, numResults: 6, stopped: TRUE
first call to combine function
evaluating call object to combine results:
fun(result.1, result.2, result.3, result.4, result.5, result.6)
returning status TRUE# Finalizar o registro dos núcleos
registerDoSEQ()O gráfico de densidade é gerado utilizando a variável BLUPS_join como base de dados. Ele exibe as densidades para cada característica (trait) usando diferentes preenchimentos e cores.
BLUPS_join_mean <- BLUPS_join %>%
group_by(trait) %>%
summarise(mean_predicted = mean(Predicted),
quantile_1 = quantile(Predicted, probs = 0.25),
quantile_2 = quantile(Predicted, probs = 0.75))
names = c("pasting_temp" = "Temperatura de empastamento (°C)",
"setback" = "Tendência a retrogradação (cP)",
"final_visc" = "Viscosidade final (cP)",
"breakdown" = "Quebra de viscosidade (cP)",
"min_visc_afheat" = "Viscosidade mínima após o aquecimento a 95 °C (cP)",
"peak_visc" = "Viscosidade de pico ou máxima (cP)")
levels(as.factor(BLUPS_join_mean$trait))[1] "breakdown" "final_visc" "min_visc_afheat" "pasting_temp"
[5] "peak_visc" "setback" BLUPS_join %>%
ggplot(aes(Predicted, after_stat(count), fill = trait, color = trait)) +
geom_density(show.legend = FALSE, alpha = 0.8) +
geom_vline(data = BLUPS_join_mean, aes(xintercept = mean_predicted), colour = "black", linetype = "dashed", show.legend = F) +
geom_vline(data = BLUPS_join_mean, aes(xintercept = quantile_1), colour = "indianred4", linetype = 4, show.legend = F) +
geom_vline(data = BLUPS_join_mean, aes(xintercept = quantile_2), colour = "indianred4", linetype = 4, show.legend = F) +
facet_wrap(vars(trait), scales = "free", strip.position = "bottom", labeller = as_labeller(names)) +
theme_classic() +
theme(strip.background = element_blank(),
strip.placement = "outside",
text = element_text(size = 15)) +
labs(y = "Density", x = "") +
scale_fill_gdocs() +
scale_color_gdocs() 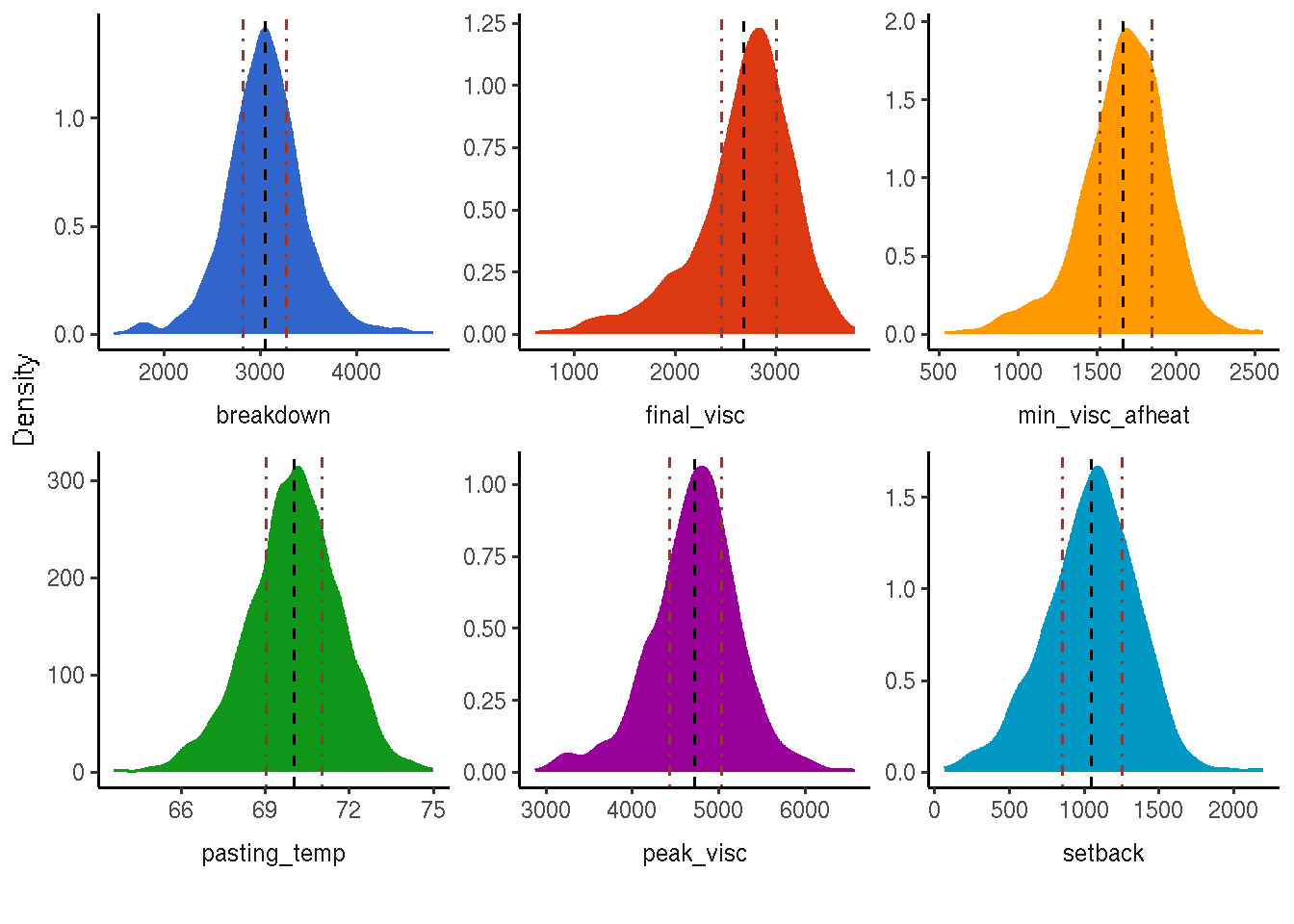
ggsave("output/density_BLUPS.tiff", width = 12, height = 8)Os parâmetros são obtidos a partir da junção dos data frames contidos em BLUPS_join$parameters usando a função merge. Os números nas colunas (exceto a primeira coluna) são arredondados para 4 casas decimais. O resultado é exibido como uma tabela formatada usando o pacote kableExtra.
parametros <- Reduce(function(x, y) merge(x, y, all = TRUE), BLUPS_join$parameters)
parametros[,-1] <- as.data.frame(lapply(parametros[,-1], function(x) round(x, 4)))
parametros %>%
kbl(escape = FALSE, align = 'c') %>%
kable_classic("hover", full_width = FALSE, position = "center", fixed_thead = TRUE)| Parameters | pasting_temp | setback | final_visc | breakdown | min_visc_afheat | peak_visc |
|---|---|---|---|---|---|---|
| Accuracy | 0.8789 | 0.9106 | 0.8972 | 8.4900e-01 | 0.8276 | 0.8468 |
| CVg | 1.2132 | 16.5315 | 9.8721 | 6.1601e+00 | 7.2323 | 5.0555 |
| CVr | 0.7077 | 6.6075 | 3.1372 | 3.7244e+00 | 3.8203 | 2.8587 |
| CV ratio | 1.7142 | 2.5019 | 3.1468 | 1.6540e+00 | 1.8931 | 1.7685 |
| GEIr2 | 0.6493 | 0.6049 | 0.6594 | 7.0760e-01 | 0.7577 | 0.7199 |
| h2mg | 0.7724 | 0.8291 | 0.8049 | 7.2070e-01 | 0.6849 | 0.7171 |
| Heritability | 0.2616 | 0.3407 | 0.3094 | 2.1410e-01 | 0.1894 | 0.2123 |
| Phenotypic variance | 2.7576 | 85726.0373 | 223611.7869 | 1.6395e+05 | 75689.7118 | 265655.1967 |
| rge | 0.8794 | 0.9174 | 0.9548 | 9.0040e-01 | 0.9348 | 0.9138 |
write.table(parametros, file = "output/parametros.csv")Os componetnes de variância são obtidos a partir da junção dos data frames contidos em BLUPS_join$vcomp usando a função merge. Os números nas colunas (exceto a primeira coluna) são arredondados para 4 casas decimais. O resultado é exibido como uma tabela formatada usando o pacote kableExtra.
vcomp <- Reduce(function(x, y) merge(x, y, all = TRUE), BLUPS_join$vcomp)
vcomp[,-1] <- as.data.frame(lapply(vcomp[,-1], function(x) round(x, 4)))
vcomp %>%
kbl(escape = FALSE, align = 'c') %>%
kable_classic("hover", full_width = FALSE, position = "center", fixed_thead = TRUE)| Group | pasting_temp | setback | final_visc | breakdown | min_visc_afheat | peak_visc |
|---|---|---|---|---|---|---|
| GEN | 0.7215 | 29208.375 | 69185.648 | 35108.15 | 14336.28 | 56391.28 |
| GEN:ENV | 1.7906 | 51851.604 | 147439.465 | 116008.28 | 57353.29 | 191232.99 |
| Residual | 0.2455 | 4666.058 | 6986.674 | 12833.62 | 4000.14 | 18030.94 |
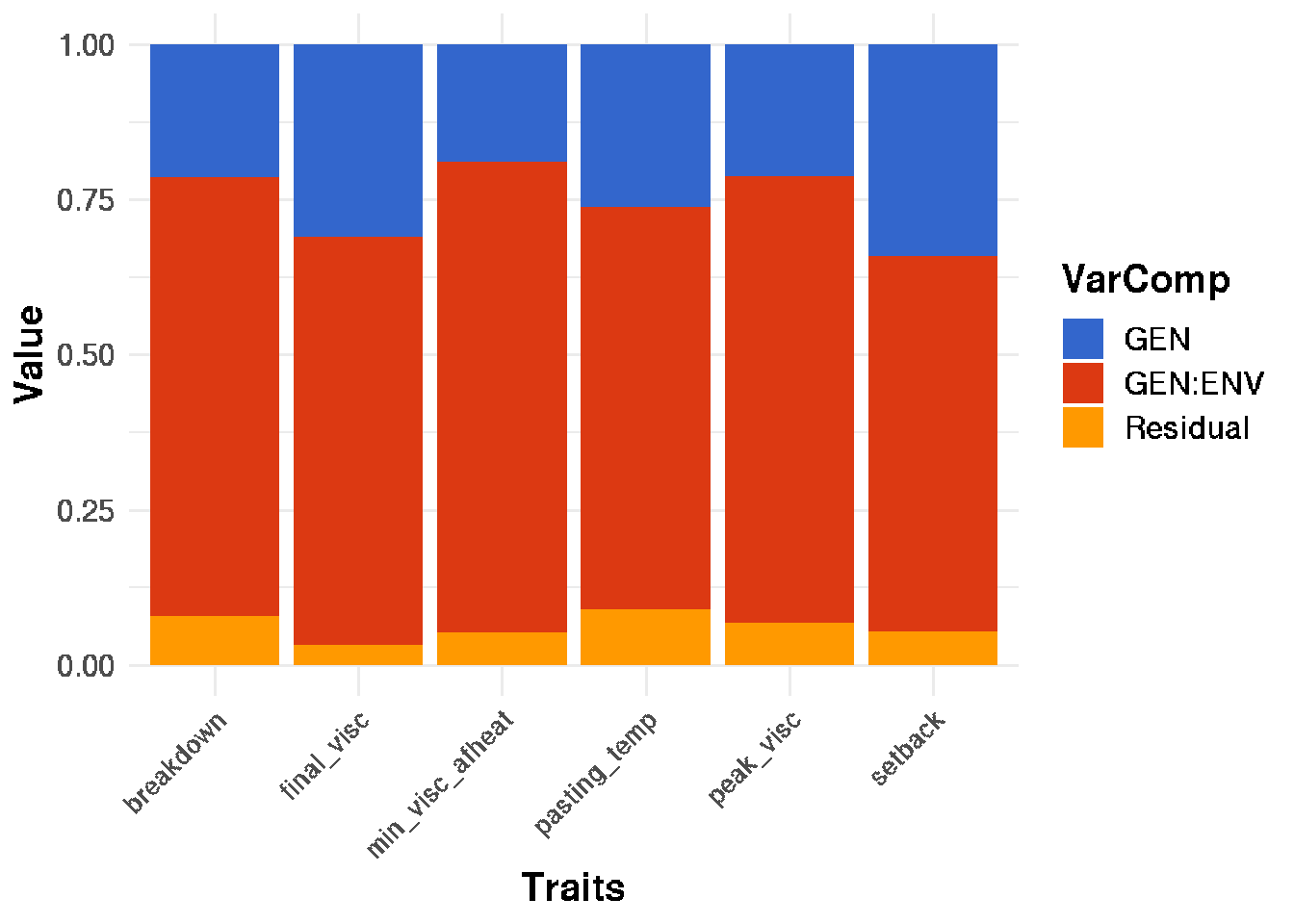
write.table(vcomp, file = "output/vcomp.csv")Plotando os componentes de variância
Neste trecho de código, estamos plotando os componentes de variância. Primeiro, usamos a função pivot_longer para transformar os dados da matriz vcomp em um formato longo, onde cada variável de coluna é mapeada para uma única coluna. Em seguida, utilizamos a função ggplot para criar o gráfico de barras empilhadas. Definimos as variáveis estéticas x, y e fill, e personalizamos as etiquetas dos eixos, a legenda e o tema visual. Por fim, salvamos o gráfico em um arquivo chamado “varcomp.tiff”.
varcomp <- vcomp %>%
pivot_longer(cols = 2:ncol(vcomp),
names_to = "Traits",
values_to = "vcov") %>%
mutate(Traits = factor(Traits, labels = c("Quebra", "Visc_final", "Visc_min", "Temp_emp", "Visc_max", "Tend_retro")))
varcomp %>%
ggplot(aes(x = Traits, y = vcov, fill = Group, by = Traits)) +
geom_col(position = "fill")+
labs(y="Value",
x="Traits",
fill = "VarComp")+
scale_fill_gdocs()+
theme_minimal()+
theme(text = element_text(size = 15, face = "bold"),
axis.text.x = element_text(
size = 10,
angle = 45,
hjust = 1,
vjust = 1
)) 
ggsave("output/varcomp.tiff", width = 12, height = 8)Salvando os BLUPs e os parametros
Neste bloco, estamos salvando os resultados dos valores genéticos melhorados preditos (BLUPs) e os parâmetros em arquivos separados. Utilizamos a função save para salvar os objetos BLUPS_join, parametros e vcomp em arquivos chamados “BLUPS.Rdata”, “parametros.Rdata” e “vcomp.Rdata”, respectivamente.
save(BLUPS_join, file = "output/BLUPS.Rdata")
save(parametros, file = "output/parametros.Rdata")
save(vcomp, file = "output/vcomp.Rdata")Correlações de Pearson
Nesta parte do código, estamos calculando e visualizando as correlações de Pearson. Primeiro, realizamos algumas transformações nos dados, selecionando as colunas relevantes do dataframe BLUPS_join, pivotando os dados para que cada variável se torne uma coluna. Em seguida, calculamos a matriz de correlação de Pearson utilizando a função cor. Por fim, arredondamos a matriz de correlação e a exibimos na saída.
phen <- BLUPS_join %>%
mutate(trait = factor(trait, labels = c("Quebra", "Visc_final", "Visc_min", "Temp_emp", "Visc_max", "Tend_retro"))) %>%
dplyr::select(trait, germplasmName, Predicted) %>%
pivot_wider(names_from = trait, values_from = Predicted) %>%
column_to_rownames(var = "germplasmName")
# Calcular a matriz de correlação de Pearson
corMat <- cor(phen, use = "pairwise.complete.obs")
# Visualizar a matriz de correlação arredondada
round(corMat, 4) Visc_max Visc_min Quebra Visc_final Tend_retro Temp_emp
Visc_max 1.0000 0.6367 0.8571 0.6485 0.5100 -0.3391
Visc_min 0.6367 1.0000 0.1486 0.8552 0.5451 -0.0795
Quebra 0.8571 0.1486 1.0000 0.2606 0.2904 -0.3816
Visc_final 0.6485 0.8552 0.2606 1.0000 0.8957 -0.1492
Tend_retro 0.5100 0.5451 0.2904 0.8957 1.0000 -0.1811
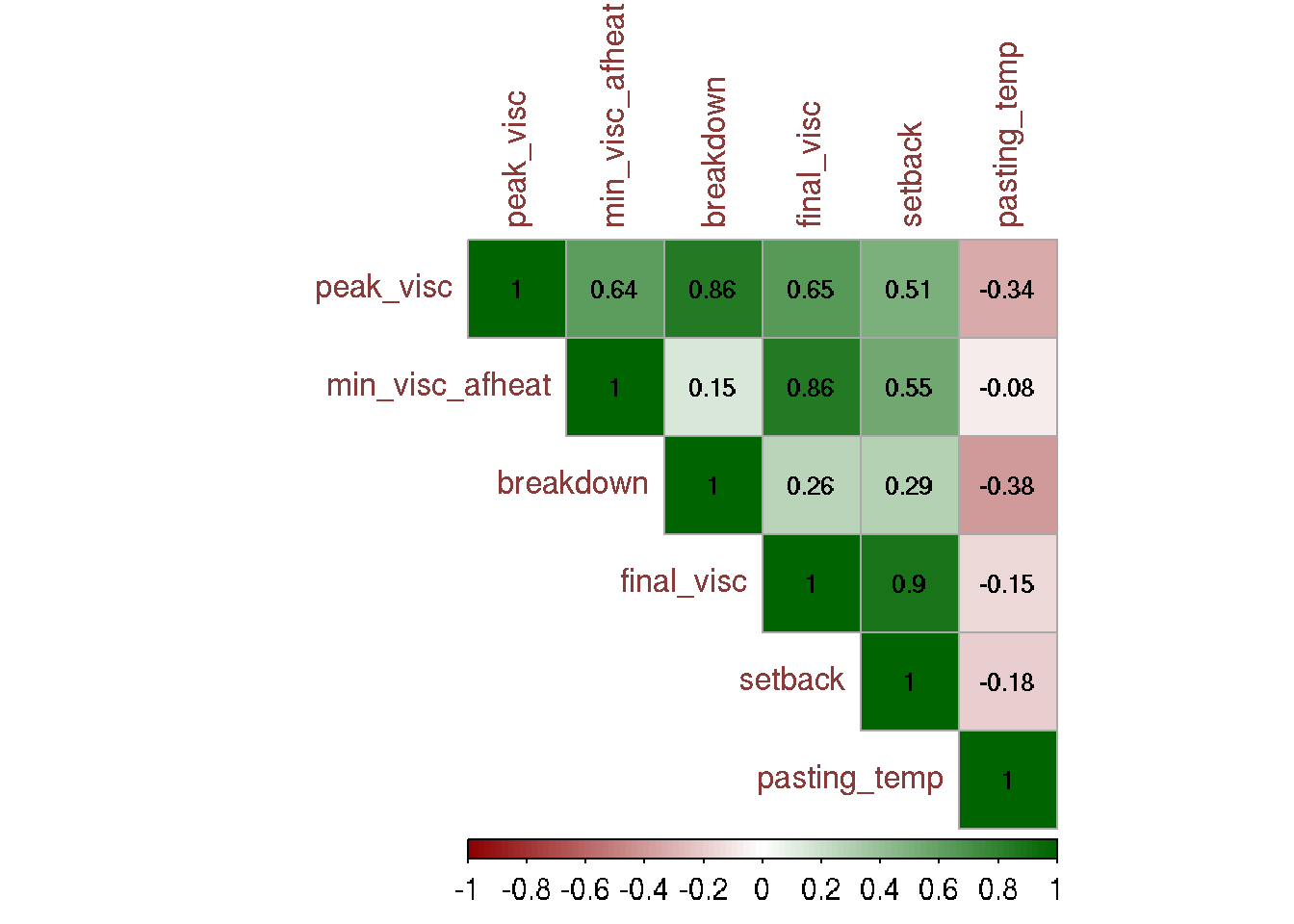
Temp_emp -0.3391 -0.0795 -0.3816 -0.1492 -0.1811 1.0000Correlograma
Neste trecho, estamos criando um correlograma para visualizar as correlações entre as variáveis. Primeiro, calculamos a matriz de correlação utilizando a função cor com o método “pearson”. Em seguida, salvamos a matriz de correlação em um arquivo chamado “Correlacao.txt”. Além disso, realizamos um teste de significância para as correlações utilizando a função cor.mtest. Por fim, plotamos o correlograma usando a função corrplot, personalizando vários parâmetros relacionados à aparência e à legenda do gráfico.
# Calcular a matriz de correlação
corr_mat <- cor(phen, method = "pearson")
# Salvar a matriz de correlação em um arquivo
write.table(corr_mat, "output/Correlacao.txt")
# Realizar o teste de significância para as correlações
res1 <- cor.mtest(phen, conf.level = 0.95)
# Plotar o correlograma
corrplot(
corr_mat,
p.mat = res1$p,
sig.level = 0.05,
type = "upper",
method = "color",
outline = TRUE,
addgrid.col = "darkgray",
addrect = 4,
rect.col = "black",
rect.lwd = 5,
cl.pos = "b",
tl.col = "indianred4",
tl.cex = 1.1,
cl.cex = 1,
addCoef.col = "black",
number.digits = 2,
number.cex = 0.8,
col = colorRampPalette(c("darkred", "white", "darkgreen"))(100)
)
DAPC
Neste trecho de código, estamos realizando a Análise de Componentes Principais Discrimitórios (DAPC). Utilizamos a função find.clusters para encontrar os clusters com base nos dados de fenótipo (phen). O parâmetro max.n define o número máximo de clusters a serem testados, n.pca especifica o número de componentes principais a serem mantidos na análise e scale indica se os dados devem ser padronizados. Em seguida, salvamos os clusters encontrados em um arquivo chamado “Clusters.txt”.
set.seed(123456)
# Encontrar os clusters usando DAPC
grp <- find.clusters(phen, max.n = 50, n.pca = 200, scale = TRUE, choose = TRUE, n.clust = 5)
# Salvar os grupos a priori em um arquivo
cluster <- data.frame(cluster = grp$grp)
cluster$germplasmName <- rownames(cluster)
# Salvar os clusters em um arquivo
write.table(cluster, 'output/Clusters.txt', sep = " ")Descrever os clusters usando DAPC
Neste bloco, estamos descrevendo os clusters encontrados utilizando DAPC. A função dapc é aplicada aos dados de fenótipo (phen) e aos clusters encontrados (grp$grp). Em seguida, usamos a função scatter para plotar o gráfico de dispersão DAPC. Os parâmetros posi.da, bg e pch são utilizados para personalizar a aparência do gráfico. Por fim, salvamos o gráfico em um arquivo “cluster.tiff”.
# Descrever os clusters usando DAPC
dapc1 <- dapc(phen, grp$grp, n.pca=3, n.da=3)
# Plotar o gráfico de dispersão DAPC
scatter(dapc1, posi.da = "bottomleft", bg = "white", pch = 17:22)
Plotar gráficos de dispersão PCA
Nesta parte do código, estamos plotando gráficos de dispersão PCA (Análise de Componentes Principais) para as combinações de componentes principais 1 e 2, 1 e 3, e 2 e 3. Utilizamos a função scatter para criar os gráficos de dispersão, definindo os componentes principais desejados e personalizando os parâmetros label.inds, posi.da, bg e pch.
PCA1x2 <- scatter(dapc1, 1, 2, label.inds = list(air = 0.5, pch = NA), posi.da = "topright")
PCA1x3 <- scatter(dapc1, 1, 3, label.inds = list(air = 0.5, pch = NA), posi.da = "bottomright")
PCA2x3 <- scatter(dapc1, 2, 3, label.inds = list(air = 0.5, pch = NA), posi.da = "bottomright")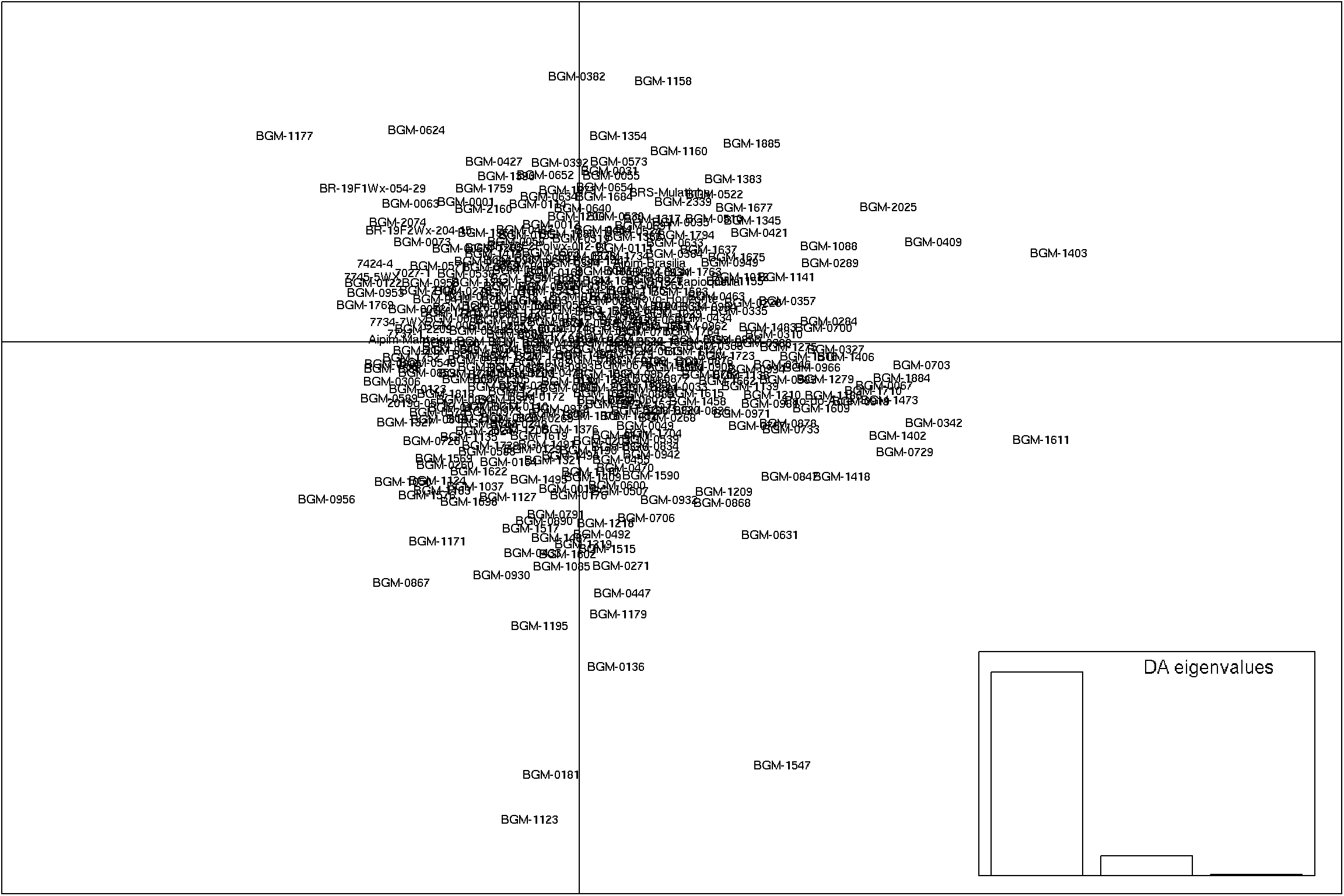
Interpretação das associações de grupos
Aqui, estamos obtendo as probabilidades a posteriori dos grupos utilizando a variável dapc1$posterior, que contém as informações sobre a atribuição de cada indivíduo a um determinado grupo. Em seguida, salvamos as probabilidades a posteriori em um arquivo chamado “Prob_a_posteriori.txt”.
# Obter as probabilidades a posteriori
probpost <- dapc1$posterior
# Salvar as probabilidades a posteriori em um arquivo
write.table(probpost, 'output/Prob_a_posteriori.txt', sep = " ")Plotar os gráficos de atribuição de grupos
Neste trecho, estamos plotando os gráficos de atribuição de grupos com base nos resultados da DAPC. Utilizamos a função assignplot para criar os gráficos e definimos o parâmetro subset para especificar o número de indivíduos a serem exibidos nos gráficos. Por fim, salvamos os grupos a priori em um arquivo chamado “Cluster_a_priori.txt”.
# Plotar os gráficos de atribuição de grupos
assignplot(dapc1, subset = 1:60)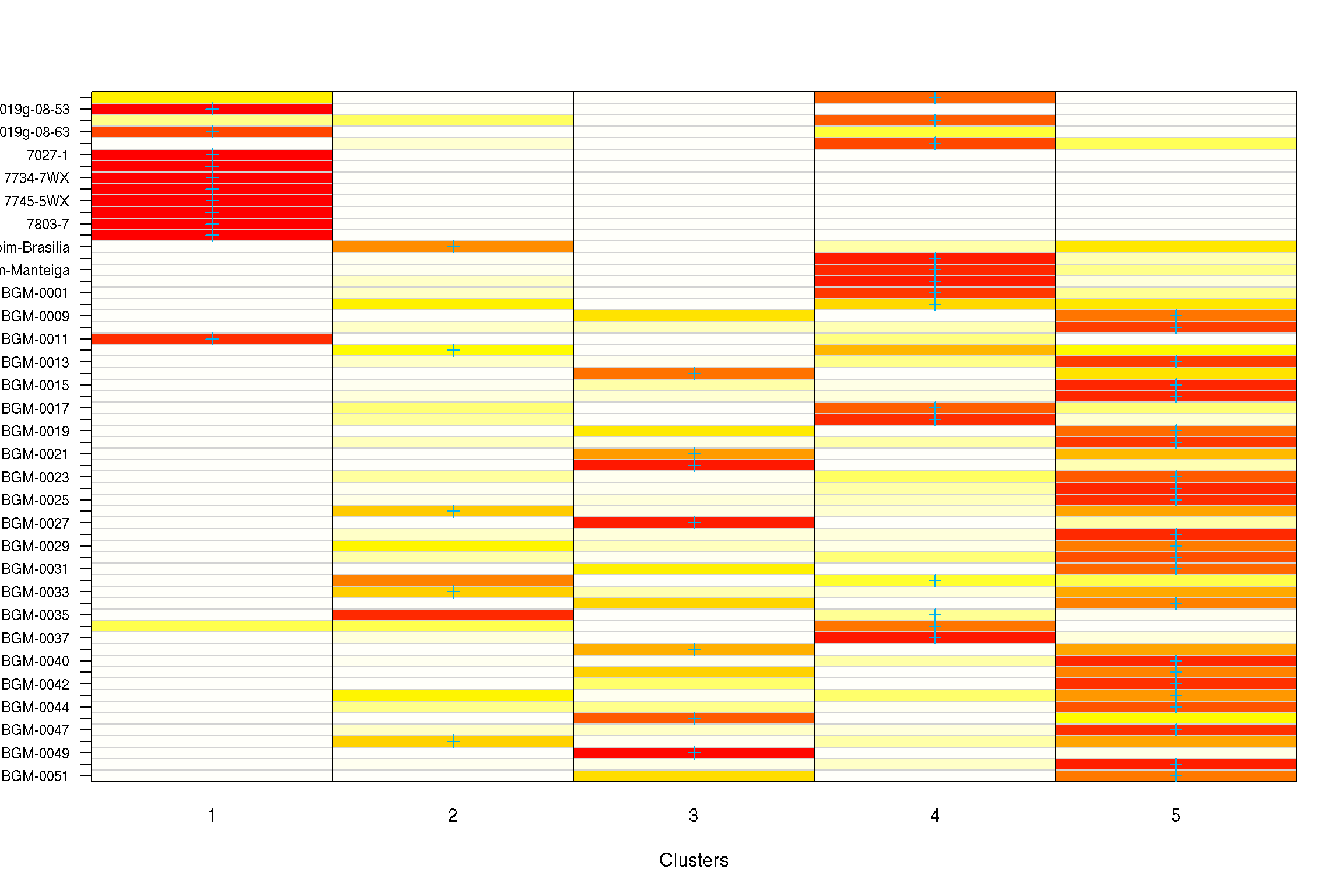
write.table(cluster, 'output/Cluster_a_priori.txt', sep = " ")Circular heatmap
Nesta parte do código, estamos criando uma circular heatmap. Primeiro, definimos as cores para a heatmap usando a função colorRamp2. Em seguida, definimos uma função padronizar para padronizar as colunas dos dados de fenótipo. Depois, aplicamos a função de padronização a todas as colunas do dataframe phen utilizando a função lapply.
Então, utilizamos a função circos.clear para limpar a plotagem anterior e configuramos alguns parâmetros com a função circos.par. Em seguida, criamos a heatmap circular com a função circos.heatmap, fornecendo os dados padronizados, a estrutura de divisão dos clusters, as cores, e personalizando os parâmetros `dend.side
# Definir as cores para a heatmap
col_fun1 = colorRamp2(
c(0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100),
c(
"blue4",
"lightblue",
"lightgreen",
"green",
"darkgreen",
"lightyellow",
"yellow",
"orange",
"orangered",
"red",
"red4"
)
)
# Calcular o número de clusters
split = structure(1:5, names = 1:5)
# Função para padronizar as colunas
padronizar <- function(x) {
min_val <- min(x)
max_val <- max(x)
(x - min_val) / (max_val - min_val) * 100
}
# Aplicar a função de padronização em todas as colunas do dataframe
phen_padronizado <- as.data.frame(lapply(phen, padronizar))
# Plotar a circular heatmap
circos.clear()
circos.par(gap.after = c(2, 2, 2, 2, 10))
circos.heatmap(
phen_padronizado,
split = split,
col = col_fun1,
dend.side = "inside",
track.height = 0.4,
dend.callback = function(dend, m, si) {
color_branches(dend, k = 1, col = split[si])
}
)
# Adicionar rótulos aos clusters
circos.track(
track.index = get.current.track.index(),
panel.fun = function(x, y) {
circos.text(
CELL_META$xcenter,
CELL_META$cell.ylim[2] + convert_y(2, "mm"),
paste0(CELL_META$sector.index),
facing = "bending.inside",
cex = 0.8,
adj = c(1, 4.5),
niceFacing = TRUE
)
},
bg.border = NA
)
# Adicionar legenda
lgd = Legend(title = "Range", col_fun = col_fun1)
grid.draw(lgd)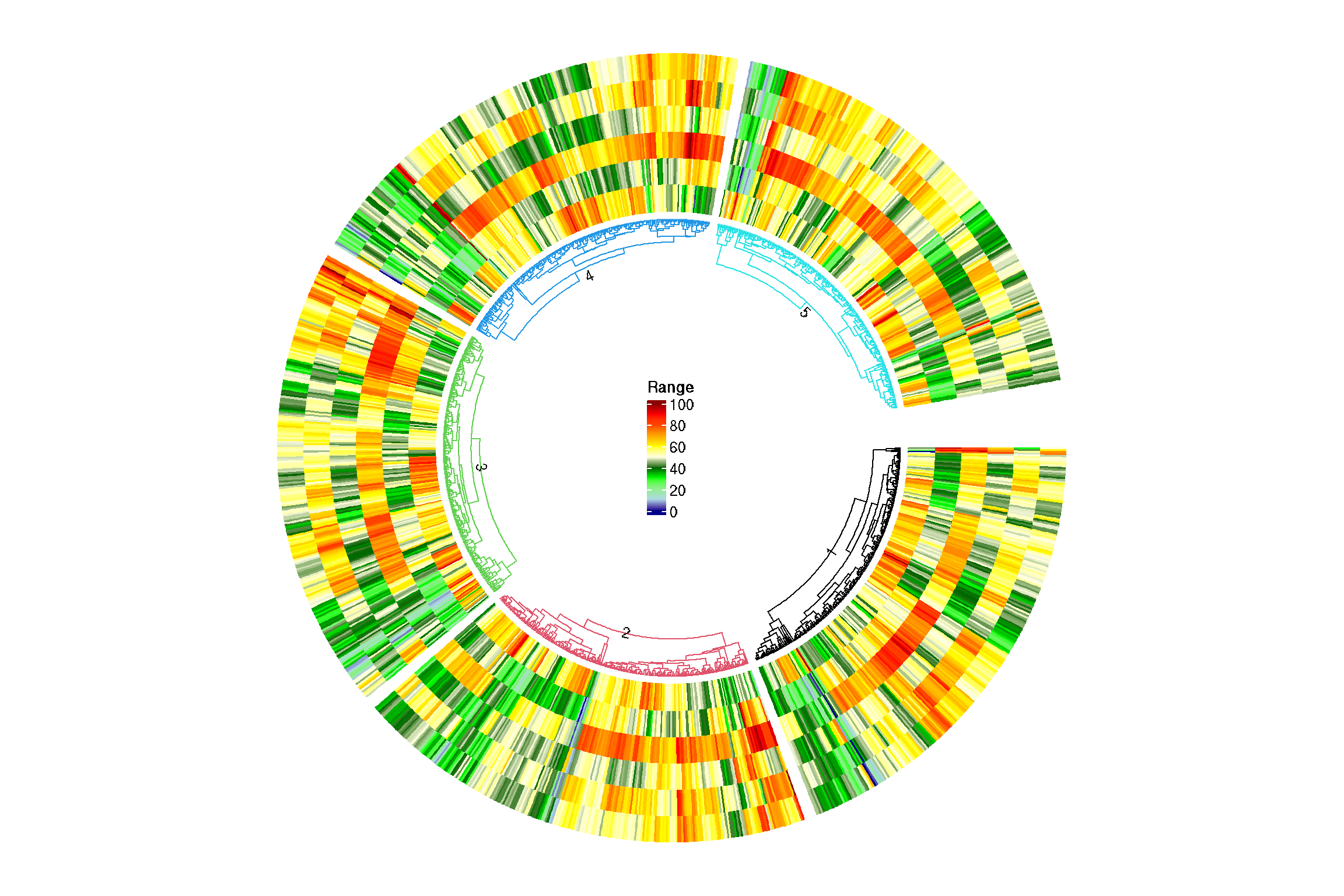
circos.clear()Analises comparativa dos cluster
Este chunk realiza o carregamento dos dados e faz um join com a variável “cluster”. O resultado é armazenado no objeto “BLUPS_join” e o arquivo é salvo como “BLUPS.RData”.
# Carrega o objeto BLUPS_join e faz um join com a variável cluster
BLUPS_join <- BLUPS_join %>%
full_join(cluster)
# Salva o objeto BLUPS_join em um arquivo RData
save(BLUPS_join, file = "output/BLUPS.RData")Cálculo das médias
São calculadas as médias dos valores das variáveis numéricas para cada combinação de “germplasmName” e “cluster”. Os resultados são armazenados no objeto “mean_germ_cluster” e são salvos em um arquivo de texto.
# Calcula as médias dos valores de cada variável numérica para cada combinação de germplasmName e cluster
mean_germ_cluster <- BLUPS_join %>%
mutate(trait = factor(trait, labels = c("Quebra", "Visc_final", "Visc_min", "Temp_emp", "Visc_max", "Tend_retro"))) %>%
pivot_wider(names_from = trait, values_from = Predicted) %>%
select(germplasmName, cluster, Visc_max:Temp_emp) %>%
group_by(germplasmName, cluster) %>%
summarise_if(is.numeric, mean, na.rm = TRUE)
# Salva as médias em um arquivo de texto
write.table(mean_germ_cluster, "output/mean_germ_cluster.txt")# Converte as variáveis cluster e trait para fatores e remove níveis não utilizados
BLUPS_join <- BLUPS_join %>%
mutate(cluster = as.factor(cluster),
trait = factor(trait)) %>%
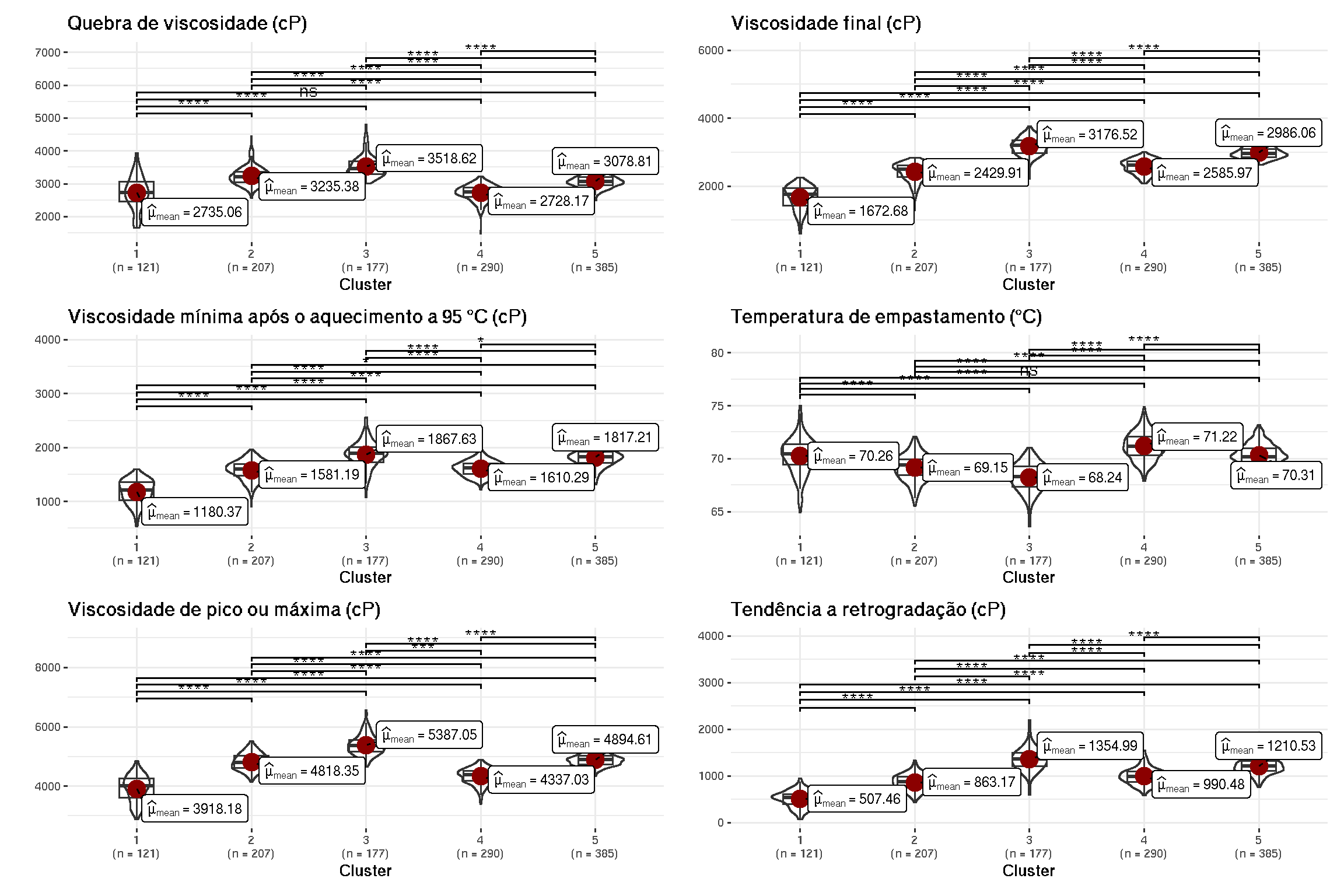
droplevels()Análise estatística e criação de gráficos
são realizados testes estatísticos e a criação de gráficos para cada nível da variável “trait”. Os resultados dos testes são armazenados nos objetos “stat.test” e “stat.test1”. Em seguida, os gráficos são criados e adicionadas as significâncias usando a função “geom_signif” do pacote “ggsignif”. Os gráficos criados anteriormente são combinados em uma única grade utilizando a função “combine_plots”. O resultado é uma grade com os gráficos para cada nível da variável “trait”.
# Cria uma lista vazia para armazenar os gráficos de cada trait
p <- list()
# Loop sobre os níveis da variável trait
for(i in levels(as.factor(BLUPS_join$trait))){
stat.test1 <- BLUPS_join %>%
filter(trait == i) %>%
t_test(Predicted ~ cluster) %>%
add_xy_position()
name <- names[[i]]
# Cria o gráfico para cada trait, adicionando as significâncias
p[[i]] <- ggbetweenstats(
data = BLUPS_join %>%
filter(trait == i),
x = cluster,
y = Predicted,
results.subtitle = FALSE,
pairwise.comparisons = FALSE,
title = name,
xlab = "Cluster",
ylab = "") +
ggsignif::geom_signif(
comparisons = stat.test1$groups,
map_signif_level = TRUE,
annotations = stat.test1$p.adj.signif,
y_position = stat.test1$y.position,
test = NULL
)
}
# Combina os gráficos em uma única grade
combine_plots(
plotlist = p,
plotgrid.args = list(nrow = 3)
)
o gráfico combinado é salvo em um arquivo TIFF com o nome “boxplot_violine.tiff” e dimensões personalizadas.
# Salva o gráfico em um arquivo TIFF
ggsave("output/boxplot_violine.tiff", width = 16, height = 24)
sessionInfo()R version 4.1.0 (2021-05-18)
Platform: x86_64-pc-linux-gnu (64-bit)
Running under: Debian GNU/Linux 10 (buster)
Matrix products: default
BLAS: /usr/local/lib/R/lib/libRblas.so
LAPACK: /usr/local/lib/R/lib/libRlapack.so
locale:
[1] LC_CTYPE=pt_BR.UTF-8 LC_NUMERIC=C
[3] LC_TIME=pt_BR.UTF-8 LC_COLLATE=pt_BR.UTF-8
[5] LC_MONETARY=pt_BR.UTF-8 LC_MESSAGES=pt_BR.UTF-8
[7] LC_PAPER=pt_BR.UTF-8 LC_NAME=C
[9] LC_ADDRESS=C LC_TELEPHONE=C
[11] LC_MEASUREMENT=pt_BR.UTF-8 LC_IDENTIFICATION=C
attached base packages:
[1] parallel grid compiler stats graphics grDevices utils
[8] datasets methods base
other attached packages:
[1] rstatix_0.7.2 ggstatsplot_0.11.1 PMCMRplus_1.9.6
[4] GGally_2.1.2 ggthemes_4.2.4 doParallel_1.0.17
[7] iterators_1.0.14 foreach_1.5.2 dendextend_1.17.1
[10] circlize_0.4.15 ComplexHeatmap_2.10.0 scatterplot3d_0.3-44
[13] gplots_3.1.3 corrplot_0.92 RColorBrewer_1.1-3
[16] adegenet_2.1.10 ade4_1.7-22 factoextra_1.0.7
[19] metan_1.18.0 kableExtra_1.3.4 DataExplorer_0.8.2
[22] lubridate_1.9.2 forcats_1.0.0 stringr_1.5.0
[25] dplyr_1.1.2 purrr_1.0.1 readr_2.1.4
[28] tidyr_1.3.0 tibble_3.2.1 ggplot2_3.4.2
[31] tidyverse_2.0.0
loaded via a namespace (and not attached):
[1] utf8_1.2.3 tidyselect_1.2.0 lme4_1.1-33
[4] htmlwidgets_1.6.2 gmp_0.7-1 munsell_0.5.0
[7] effectsize_0.8.3 ragg_1.2.5 codetools_0.2-18
[10] withr_2.5.0 colorspace_2.1-0 highr_0.10
[13] knitr_1.43 rstudioapi_0.14 stats4_4.1.0
[16] ggsignif_0.6.4 labeling_0.4.2 emmeans_1.8.6
[19] git2r_0.32.0 polyclip_1.10-4 farver_2.1.1
[22] datawizard_0.7.1 rprojroot_2.0.3 coda_0.19-4
[25] vctrs_0.6.2 generics_0.1.3 xfun_0.39
[28] timechange_0.2.0 BWStest_0.2.2 R6_2.5.1
[31] clue_0.3-64 bitops_1.0-7 cachem_1.0.8
[34] reshape_0.8.9 promises_1.2.0.1 networkD3_0.4
[37] scales_1.2.1 gtable_0.3.3 multcompView_0.1-9
[40] workflowr_1.7.0 rlang_1.1.1 zeallot_0.1.0
[43] systemfonts_1.0.4 GlobalOptions_0.1.2 splines_4.1.0
[46] prismatic_1.1.1 broom_1.0.4 yaml_2.3.7
[49] reshape2_1.4.4 abind_1.4-5 backports_1.4.1
[52] httpuv_1.6.11 tools_4.1.0 ellipsis_0.3.2
[55] jquerylib_0.1.4 BiocGenerics_0.40.0 Rcpp_1.0.10
[58] plyr_1.8.8 GetoptLong_1.0.5 viridis_0.6.3
[61] correlation_0.8.4 S4Vectors_0.32.4 ggrepel_0.9.3
[64] cluster_2.1.2 fs_1.6.2 magrittr_2.0.3
[67] data.table_1.14.8 lmerTest_3.1-3 mvtnorm_1.1-3
[70] whisker_0.4.1 matrixStats_1.0.0 hms_1.1.3
[73] patchwork_1.1.2 mime_0.12 evaluate_0.21
[76] xtable_1.8-4 readxl_1.4.2 IRanges_2.28.0
[79] gridExtra_2.3 shape_1.4.6 KernSmooth_2.23-20
[82] crayon_1.5.2 minqa_1.2.5 htmltools_0.5.5
[85] mgcv_1.8-35 later_1.3.1 tzdb_0.4.0
[88] SuppDists_1.1-9.7 kSamples_1.2-9 tweenr_2.0.2
[91] MASS_7.3-54 boot_1.3-28 Matrix_1.5-4.1
[94] car_3.1-2 permute_0.9-7 cli_3.6.1
[97] insight_0.19.2 igraph_1.4.3 pkgconfig_2.0.3
[100] statsExpressions_1.5.1 numDeriv_2016.8-1.1 xml2_1.3.4
[103] paletteer_1.5.0 svglite_2.1.1 bslib_0.4.2
[106] webshot_0.5.4 estimability_1.4.1 rvest_1.0.3
[109] snakecase_0.11.0 digest_0.6.31 parameters_0.21.1
[112] janitor_2.2.0 vegan_2.6-4 cellranger_1.1.0
[115] rmarkdown_2.22 shiny_1.7.4 gtools_3.9.4
[118] rjson_0.2.21 nloptr_2.0.3 lifecycle_1.0.3
[121] nlme_3.1-152 jsonlite_1.8.4 carData_3.0-5
[124] seqinr_4.2-30 viridisLite_0.4.2 fansi_1.0.4
[127] pillar_1.9.0 lattice_0.20-44 fastmap_1.1.1
[130] httr_1.4.6 glue_1.6.2 bayestestR_0.13.1
[133] png_0.1-8 ggforce_0.4.1 stringi_1.7.12
[136] sass_0.4.6 rematch2_2.1.2 textshaping_0.3.6
[139] caTools_1.18.2 memoise_2.0.1 mathjaxr_1.6-0
[142] Rmpfr_0.9-2 ape_5.7-1 Weverton Gomes da Costa, Pós-Doutorando, Embrapa Mandioca e Fruticultura, wevertonufv@gmail.com↩︎